This article follows on my previous introductions to uncertainty and uncertainty budgets. It goes into more detail about some of the more tricky aspects of uncertainty budgets. I first explain what sensitivity coefficients are and then use examples to show exactly how sensitivity coefficients can be calculated and used within an uncertainty budget. Read the full article published on engineering.com…
Gage Studies and Gage R&R on engineering.com
If you’ve ever been involved with an industrial measurement process, chances are you’ve come across Gage studies and in particular Gage Repeatability and Reproducibility (Gage R&R). These tests are used to determine the accuracy of measurements. In this article I provide an overview of these studies and how they relate to other methods such as uncertainty evaluation. Read the full article on engineering.com…
Calculating Your Uncertainty Budget… on engineering.com
This is a detailed article explaining how you can calculate an uncertainty budget. It follows my previous introduction to Metrology and Quality in Manufacturing. My previous article introduced the idea that all measurements have uncertainty. This uncertainty stems from different sources, including repeatability, calibration and the environment. To find the uncertainty of a measurement result, we must first estimate the contribution from each source and then calculate the combined uncertainty. Uncertainty budgets provide a relatively simple way to do this. Read the full article, published on engineering.com, here…
Uncertainty of Product Verification study with Rolls-Royce
This open access paper shows how easily misunderstood uncertainty of product verification can be. This comes from our ground breaking work with Rolls-Royce. We found that the uncertainty of the instrument was only a very small part of the uncertainty of measurement. Before we optimized the process most of the uncertainty came from tooling. After improved tooling was designed the dominant source was thermal expansion of the engine. So we couldn’t improve it any more without temperature control in the factory. The lessons of this study are far reaching. Most importantly, the uncertainty of measurements on a product may be many times higher than the individual coordinate measurements that an instrument records. Tooling, datum structures and thermal expansion may be far more significant than the instrument used.
Paper Title: Uncertainty of measurement for large product verification: evaluation of large aero gas turbine engine datums
Authors: J E Muelaner1, Z Wang1, P S Keogh1, J Brownell2 and D Fisher2
1) University of Bath 2) Rolls-Royce plc
Published in: Measurement Science and Technology, 2016, Issue 27(11): p. 1-12
Abstract: Understanding the uncertainty of dimensional measurements for large products such as aircraft, spacecraft and wind turbines is fundamental to improving efficiency in these products. Much work has been done to ascertain the uncertainty associated with the main types of instruments used, based on laser tracking and photogrammetry, and the propagation of this uncertainty through networked measurements. Unfortunately this is not sufficient to understand the combined uncertainty of industrial measurements, which include secondary tooling and datum structures used to locate the coordinate frame. This paper presents for the first time a complete evaluation of the uncertainty of large scale industrial measurement processes. Generic analysis and design rules are proven through uncertainty evaluation and optimization for the measurement of a large aero gas turbine engine. This shows how the instrument uncertainty can be considered to be negligible. Before optimization the dominant source of uncertainty was the tooling design, after optimization the dominant source was thermal expansion of the engine; meaning that no further improvement can be made without measurement in a temperature controlled environment. These results will have a significant impact on the ability of aircraft and wind turbines to improve efficiency and therefore reduce carbon emissions, as well as the improved reliability of these products.
Study of the Accuracy of Photogrammetry systems published in The Photogrammetric Record
Title: Comparative Performance between Two Photogrammetric Systems and a Reference Laser Tracker Network for Large-Volume Industrial Measurement
This study compared two photogrammetry systems against a laser tracker. This provides an independent study of the accuracy of photogrammetry systems.
Authors: O C Martin, S Robson, A Kayani, J E Muelaner, V Dhokia, P G Maropoulos
Published in: The Photogrammetric Record, 2016, Issue 31(155): p. 348-360
Abstract: This paper determines the capability of two photogrammetric systems in terms of their measurement uncertainty in an industrial context. The first system – V-STARS inca3 from Geodetic Systems Inc. – is a commercially available measurement solution. The second system comprises an off-the-shelf Nikon D700 digital camera fitted with a 28 mm Nikkor lens and the research-based Vision Measurement Software (VMS). The uncertainty estimate of these two systems is determined with reference to a calibrated constellation of points determined by a Leica AT401 laser tracker. The calibrated points have an average associated standard uncertainty of 12·4 μm, spanning a maximum distance of approximately 14·5 m. Subsequently, the two systems’ uncertainty was determined. V-STARS inca3 had an estimated standard uncertainty of 43·1 μm, thus outperforming its manufacturer’s specification; the D700/VMS combination achieved a standard uncertainty of 187 μm.
Improving Error Models of Machine Tools with Metrology Data
Typically a machine tool is calibrated once a year to update the machine tool error model, at best! This will result in compensations which are less than optimal. There is however a better way, using data from measured parts and rapid checks capability can be greatly improved. Leverage the abundance of measurement data available in a modern production system to identify machine tool errors without down-time… You can download the full paper here.
Authors: J M Flynn, J E Muelaner, V Dhokia, S T Newman
Published in: Procedia CIRP, vol. 52, pages 204 – 209
Abstract: As the manufacturing community embraces the use of a variety of metrology solutions, the availability and quantity of measurement data is increasing. The tendency towards connectedness between manufacturing resources may also provide a mechanism for communication and exploitation of metrology data like never before. This research aims to provide an insight into the opportunities that are associated with accessible, abundant and communicable manufacturing metrology data. Issues are raised and critically discussed in relation to one particular aspect of manufacturing metrology, namely, machine tool accuracy verification and calibration. Specifically, a methodology for relating CMM part measurements to individual machine tool geometric error sources is described. A novel Monte Carlo simulation-based method is used to estimate previously unmeasured error values without the use of further testing. Using this method, the advantage of using previously captured verification and calibration data to identify likely causes of part defects is shown. It is envisaged that the proposed method can be used to instruct targeted machine tool verification and calibration routines to reduce the number of tests required to monitor a machine tool’s health. By using targeted tests, the need to measure all machine error sources is reduced, which in turn can improve productivity by reducing machine tool downtime.
Uncertainty Evaluation Method for Axi-Symmetric Measurement Machines published in Int J of Metrology & Quality Eng.
Title: Uncertainty Evaluation Method for Axi-Symmetric Measurement Machines
Axi-Symmetric Measurement Machines measure roundness, axial runout and coning. A complete uncertainty evaluation procedure is given . You can download the full paper here.
Authors: J E Muelaner, P S Keogh
Journal: Int J of Metrology & Quality Eng., 7(2)
Abstract: This paper describes a method of uncertainty evaluation for axi-symmetric measurement machines. Specialized measuring machines for the inspection of axisymmetric components enable the measurement of properties such as roundness (radial runout), axial runout and coning. These machines typically consist of a rotary table and a number of contact measurement probes located on slideways. Sources of uncertainty include the probe calibration process, probe repeatability, probe alignment, geometric errors in the rotary table, the dimensional stability of the structure holding the probes and form errors in the reference hemisphere which is used to calibrate the system. The generic method is described and an evaluation of an industrial machine is described as a worked example. Expanded uncertainties, at 95% confidence, were then calculated for the measurement of; radial runout (1.2 µm with a plunger probe or 1.7 µm with a lever probe); axial runout (1.2 µm with a plunger probe or 1.5 µm with a lever probe); and coning/swash (0.44 arc seconds with a plunger probe or 0.60 arc seconds with a lever probe).
Gage Repeatability and Reproducibility, Gage R&R in Excel
A Gage Repeatability and Reproducibility (Gage R&R) study is a great way to understand the variation in a measurement process. You don’t need special software like Minitab. You can do Gage R&R in Excel just fine. No macros or special functions are required but it does take a while to set everything up. If you just want to do Gage R&R in Excel quickly and reliably then save yourself a headache and get my Gage R&R Excel add-in. Many people using special software just plug in the numbers without understanding what is being calculated. If you follow this article you will fully understand the maths. But when it’s time to perform actual Gage R&R studies, I strongly recommend you do use a validated tool such as Minitab or my add-in.
What’s covered in this article:
- What is Gage R&R?
- Calculating Gage R&R using an Excel Spreadsheet
- Step 1: Calculate the Grand Mean (the mean of all measurement values)
- Step 2: For each measurement calculate the mean for all measurements with the same Part ID, the same Operator ID
and the same Part and Operator ID’s - Step 3: For each measurement calculate the squared difference between means
- Step 4: Sum each of the squared differences for all measurements
- Step 5: Calculate Part Operator Interaction
- Step 6: Calculate the Mean of the Squared Differences
- Step 7: Calculate the significance of Part Operator interaction
- Step 8: Decided whether to include Part Operator interaction in
What is Gage R&R?
The variation in measurement results, or precision, is affected by many factors such as:
- The operator
- The equipment used
- The calibration of the equipment
- The
environment The time elapsed between measurements
As more of these factors are varied it can be expected that the variation in measurement results will increase. This leads to two extreme conditions of precision; repeatability and reproducibility. Repeatability is the minimum condition for precision in which the above factors are held constant while reproducibility is the maximum condition in which all of these factors vary. Often some intermediate measure of precision is relevant in which all of the possible factors effecting reproducibility are not varied since some of these will be maintained constant for the process under consideration.
When designing a Gage R&R study you need to decide which reproducibility conditions will vary for the actual measurement process. Will different operators
A typical Crossed Gage R&R study might involve 10 parts each being measured 3 times by 3 different operators in their own work area. By applying Analysis of Variance (ANOVA) it is then possible to determine the individual variance components due to the part variation, the repeatability of measurements and the reproducibility between different operators. The total Gage R&R variance is the sum of the variance for repeatability and the variance for reproducibility; this is an important component of a full uncertainty evaluation.
The calculation of variance components and standard deviations using ANOVA is equivalent to calculating variance and standard deviation for a single variable but it enables multiple sources of variation to be individually quantified which are simultaneously influencing a single data set.
A Gage R&R study should be used as part of a full uncertainty analysis and included in an uncertainty budget. This Hybrid Measurement Systems Analysis and Uncertainty of Measurement Approach for Industrial Measurement is a relatively new approach which enables conformance to be prove with known statistical confidence.
Calculating Gage R&R in Excel
Before reading the detailed description of the calculations it is recommended that you download the Gage R&R Spreadsheet Example. This can then be referred to while reading the article and once you have a full understanding of how it works it will be easy to adapt it to your own studies. For clarity the spreadsheet only uses 5 parts, 2 operators and 2 measurements per part/operator. For a real study at least 10 parts, 3 operators and 3 measurements is recommended.
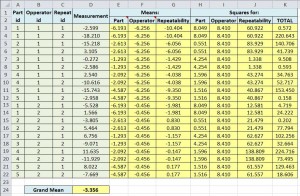
The example spreadsheet is divided into two tables to make things clearer. The first table, shown below, has a separate row for each measurement made in the study. Columns A to D contain the inputs recorded for the measurements in the study. For each
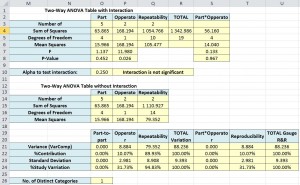
The second table in the example spreadsheet, shown below, is used to calculate various values which summarize the complete data set. Intermediate calculations are used to finally calculate the variance components and standard deviations for the; variation between the actual parts; repeatability; the reproducibility due to different operators; and some other sources explained in the following sections.
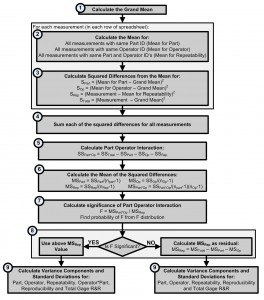
The Gage R&R ANOVA calculations follow these steps (with links to the detailed explanations below):
In Table 1:
- Step 1: Calculate the Grand Mean (the mean of all measurement values)
- Step 2: For each measurement calculate the mean for all measurements with the same Part ID, the same Operator ID and the same Part and Operator ID’s
- Step 3: For each measurement calculate the squared difference between means
In Table 2:
- Step 4: Sum each of the squared differences for all measurements
- Step 5: Calculate Part Operator Interaction
- Step 6: Calculate the Mean of the Squared Differences
- Step 7: Calculate the significance of Part Operator interaction
- Step 8: Decided whether to include Part Operator interaction in the model and if not calculate a different value for Mean Squared Difference for Repeatability
- Step 9: Calculate Variance Components and Standard Deviations
The figure below gives a slightly more detailed overview of the Gage R&R ANOVA calculations before the full explanation is given for each below.
If this all seems a bit too much effort then you might prefer to simply download my Gage R&R Excel add-in. This puts all of these steps into a simple Excel formula which quickly and simply gives you results from a Gage R&R Study.
Step 1: Calculate the Grand Mean (the mean of all measurement values)
The Grand Mean is first calculated (Cell D24) which is simply the mean for all measurement values.
Step 2: For each measurement calculate the mean for all measurements with the same Part ID, the same Operator ID and the same Part and Operator ID’s
In the “Gage R&R Spreadsheet Example.xls” the mean for all measurements with the same Part ID is calculated in column E and with the same operator ID in column F. In column G the mean for each ‘factor level’ is calculated which is the mean for all measurements with the same part and operator ID’s and is used to represent repeatability.
The formula used to calculate the Mean for Part is repeated in column E of the spreadsheet on each row so the mean for the part is given for each measurement made, the formula in cell E3 looks like this:
Mean for Part:
=SUMIF( A$3:A$22, "="&A3, D$3:D$22 ) / COUNTIF( A$3:A$22, "="&A3 )It uses the SUMIF function to compare the Part ID for the current row (A3) with the Part ID for each row in turn (A$3:A$22). This formula is copied down each row, for all the rows where the Part ID is the same as the current row the measurement values (D$3:D$22) are summed. The COUNTIF function is then used to count the number of measurements with the same Part ID as the current measurement. Dividing the result of the SUMIF by the result of the COUNTIF gives the mean average for all measurement values with the same Part ID as the current measurement. All measurements with the same Part ID will have the same value for Mean for Part.
The formula used to calculate the Mean for Operator is the same as that used for Mean for Part with the only difference that the Operator ID is substituted for the Part ID:
Mean for Operator:
=SUMIF($B$3:$B$22,"="&B3,$D$3:$D$22) / COUNTIF($B$3:$B$22,"="&B3)The formula used to calculate the Mean for Each Factor Level which represents repeatability is slightly different to that used for the Part and the Operator. SUMIFS is used in place of the SUMIF function to test for multiple criteria. In this case we need to sum the measurement values (D$3:D$22) if the Part ID’s (A$3:A$22) match the Part ID for the current measurement (A3) and the Operator ID’s (B$3:B$22) match the Operator ID for the current measurement (B3). The COUNTIFS is then used to divide the sum by the number of measurements matching this same condition. So for each measurement the mean of all measurements of the same part by the same operator is found.
Mean for Each Factor Level:
=SUMIFS(D$3:D$22,A$3:A$22,"="&A3,B$3:B$22,"="&B3)/COUNTIFS($A$3:$A$22,"="&A3,$B$3:$B$22,"="&B3)Step 3: For each measurement calculate the squared difference between means
Once the relevant means for each measurement value have been calculated the grand mean is subtracted from each one and the difference is squared. These values are given in columns H, I and J. The total sum of squared differences, given in column K, is simply the square of the difference between each individual measurement value and the grand mean.
Step 4: Sum each of the squared differences for all measurements
The final stage in calculating the sums of the squared differences is simply to sum the values in the columns H, I, J and K, the resulting sums are given in Table 2 of the example spreadsheet in cells O3, P3, Q3 and R3 respectively.
These sums of squared differences are normally represented using the below equations for the part (
where nOp is the number of operators, nRep is the number of replicate measurements of each part by each operator, nPart is the number of parts, x̄ is the grand mean, x̄i is the mean for each part, x̄j is the mean for each operator, xijk is each observation and x̄ij is the mean for each factor level. When following the spreadsheet method of calculation the n terms are not explicitly required since each squared difference is automatically repeated across the rows for the number of measurements meeting each condition.
The sum of the squared differences for part by operator interaction (SSPart*Op) is the residual variation given by
Step 5: Calculate Part Operator Interaction
The sum of the squared differences for part by operator interaction, given in cell S3, is simply the residual variation given by:
Step 6: Calculate the Mean of the Squared Differences
The numbers of different parts (nPart), of operators (nOp) and of repetitions of the measurement of each part by each operator (nRep) are given in cells O3, P3 and Q3 respectively. This is calculated in Excel by counting the number of unique number values in the column containing the ID numbers (not counting blank cells or text values) which, for the Part ID is given by
=SUM(IF(FREQUENCY(A3:A22,A3:A22)>0,1))These values are then used to calculate the degrees of freedom (DF) for each factor using the below equations and given in cells O5, P5, Q5, R5 and S5 of the example spreadsheet.
It is then possible to calculate the mean squared difference for each factor by dividing the corresponding sum of the squared differences by the degrees of freedom. These values are given in O6, P6, Q6 and S6 on the example spreadsheet. At this stage the similarity with the calculation of a simple variance should be quite apparent.
Step 7: Calculate the significance of Part Operator interaction
The significance of the part by operator interaction on variation should then be determined by first calculating the F-statistic (in cell S7) which is the Mean Squared value for Part by Operator interaction divided by the Mean Squared value for Repeatability.
The probability of FPart*Op being significant is then calculated in cell S8 by looking up the probability from an F-distribution where the value of the F-statistic is given in cell S7, the degrees of freedom for the numerator is given in S5, degrees of freedom for the denominator is in Q5 and a cumulative distribution is used:
=1-F.DIST(S7,S5,Q5,TRUE)If the interaction is significant then the above values of the mean squared differences are used to calculate components of variance. The alpha value to test against is given in cell O10 and an if statement is used in P10 to state whether the interaction is significant.
Step 8: Decide whether to include Part Operator interaction in the model and if not calculate a different value for Mean Squared Difference for Repeatability
If the interaction is not significant then the same values are used for MSPart and MSOP but MSPart*Op is ignored and MSRep is now the residual variation and therefore SSRep is calculated as
This value is calculated in cell Q15. When calculating the variance components, in Step 9 below, IF statements are used in cells O21, P21, Q21 and S21 to determine which value for SSRep should be used.
Step 9: Calculate Variance Components and Standard Deviations
The variance components for each factor can now be calculated. In some cases the equation used depends on whether Part by Operator interaction is included in the model and in these cases an IF statement is used to check the value in P10 and select the correct equation accordingly.
Variance Component for Part-to-Part Variation
When the part by operator interaction is significant the variance component for part-to-part variation (σ2Part) is calculated using
When the part by operator interaction is not significant the variance component for part-to-part variation is calculated using
It is possible for these equations to return a negative value in which case the value should be set to zero, therefore the variance component for part by operator interaction is calculated in cell O21 using the formula:
=MAX(0,IF(P10="Interaction is not significant",(O17-Q17)/(P14*Q14),(O6-S6)/(P3*Q3)))Variance Component for Variation due to Operator
When the part by operator interaction is significant the variance component for operator variation (σ2Op) is calculated using
When the part by operator interaction is not significant it is given by
The Excel formula again selects the correct equation and sets negative values to zero:
=MAX(0,IF(P10="Interaction is not significant",(P17-Q17)/(O14*Q14),(P6-S6)/(O3*Q3)))Variance Component for Repeatability
The variance component for repeatability (σ2Rep) is calculated using
Variance Component for Part by Operator Interaction
The variance component for part by operator interaction (σ2Part*Op) is given by
Since this is only included when this factor is significant and negative values are set to zero the Excel function is
=MAX(0,IF(P10=”Interaction is not significant”,0,(S6-Q6)/Q3))
Variance Component for Reproducibility
When the part by operator interaction is not significant the variance component for reproducibility (σ2Reprod) is equal to the operator variation (σ2Op). When there is significant interaction it is given by
Variance Component for Total Gage R&R
The total Gage R&R (σ2GRR) is the sum of repeatability and reproducibility.
Total Process Variation
The total process variation (σ2Tot) is the sum of total Gage R&R and part-to-part variation.
Standard Deviations
The standard deviations for each factor are simply the square root of the corresponding variance component. Hopefully, working through this process has given you a deeper understanding of how the Gage R&R calculations work. I would not, however, recommend using this approach to analyze production data. There are too many steps leaving room for human error. If you want a verified, low-cost and easy to use way to analyse Gage R&R data in Excel then I’d recommend having a look at my simple add-in for Excel: